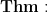 Let
Let 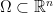 is a bounded
is a bounded 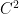 domain. Fix
domain. Fix  ,
,  is a function in
is a function in 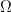 such that
such that 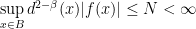 , where
, where  is the distance function. Then
is the distance function. Then
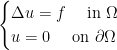
has a unique solution  satisfying
satisfying
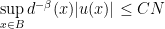
where the constant 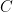 depends only on
depends only on 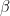 and
and 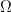 .
.
Firstly, recall some basic properties of distance function. By lemma 14.16 in GT’s book, if 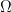 is
is 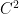 and bounded, there is a neighborhood of
and bounded, there is a neighborhood of 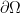 in
in 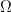 , say
, say  , such that
, such that 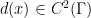 . And
. And 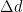 is bounded in
is bounded in  .
.

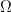 is
is 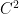 means there exists
means there exists 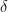 such that
such that  is
is 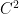 in
in 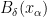 for any
for any 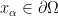 .
.
Suppose 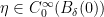 with
with 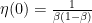 . Denote
. Denote  .
.
Fix  ,
,

![\displaystyle =\left[\beta(\beta-1)d^{\beta-2}|\nabla d|^2+\beta d^{\beta-1}\Delta d\right]\eta_{\alpha}+2\beta d^{\beta-1}\nabla d\cdot\nabla\eta_\alpha+d^\beta\Delta\eta_\alpha](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%3D%5Cleft%5B%5Cbeta%28%5Cbeta-1%29d%5E%7B%5Cbeta-2%7D%7C%5Cnabla+d%7C%5E2%2B%5Cbeta+d%5E%7B%5Cbeta-1%7D%5CDelta+d%5Cright%5D%5Ceta_%7B%5Calpha%7D%2B2%5Cbeta+d%5E%7B%5Cbeta-1%7D%5Cnabla+d%5Ccdot%5Cnabla%5Ceta_%5Calpha%2Bd%5E%5Cbeta%5CDelta%5Ceta_%5Calpha&bg=ffffff&fg=000000&s=0&c=20201002)
![=\displaystyle -d^{\beta-2}\left[\beta(1-\beta)\eta_\alpha-\beta d\Delta d-2\beta d\nabla d\cdot\nabla\eta_\alpha-d^2\Delta\eta_\alpha\right]](https://s0.wp.com/latex.php?latex=%3D%5Cdisplaystyle+-d%5E%7B%5Cbeta-2%7D%5Cleft%5B%5Cbeta%281-%5Cbeta%29%5Ceta_%5Calpha-%5Cbeta+d%5CDelta+d-2%5Cbeta+d%5Cnabla+d%5Ccdot%5Cnabla%5Ceta_%5Calpha-d%5E2%5CDelta%5Ceta_%5Calpha%5Cright%5D&bg=ffffff&fg=000000&s=0&c=20201002)

 if
if 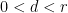 small enough.
small enough.
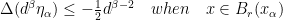
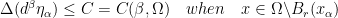
Since  is compact, there exists finitely many
is compact, there exists finitely many  such that
such that 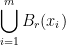 covers
covers 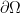 . Let
. Let 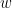 is solution of
is solution of 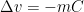 in
in 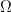 and
and 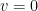 on
on 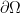 .
.
Define 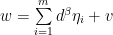 , then
, then 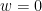 on
on 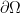 and
and 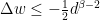 in
in 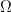 . So
. So
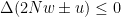 in
in 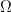 and
and  on
on 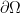
Consequently, by the maximum principle,

Since  has an upper bound only depends on the geometry of
has an upper bound only depends on the geometry of 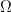 and
and  , we only need to prove
, we only need to prove  when
when  is near the boundary, where
is near the boundary, where  . Note that
. Note that
![\displaystyle \Delta(d^\beta)=d^{\beta-2}[\beta(\beta-1)+\beta d\Delta d]\rightarrow -\infty](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%5CDelta%28d%5E%5Cbeta%29%3Dd%5E%7B%5Cbeta-2%7D%5B%5Cbeta%28%5Cbeta-1%29%2B%5Cbeta+d%5CDelta+d%5D%5Crightarrow+-%5Cinfty&bg=ffffff&fg=000000&s=0&c=20201002) uniformly as
uniformly as 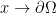
So there exists a neighborhood 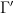 of
of 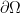 such that
such that  and
and 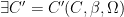
 in
in 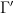 and
and 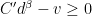 on
on 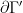
By the maximum principle,  in
in 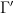 .
.

 Gilbarg, Trudinger. Chapter 4, exercise 4.6. p71
Gilbarg, Trudinger. Chapter 4, exercise 4.6. p71
Also see, J.H. Michael. A general theory for linear elliptic partial differential equations. 1977
Gary M. Lieberman. Elliptic equations with strongly singular lower order terms. 2008
is a complete Riemannian manifold.
define
. Obviously
is continuous, what can we say about the smoothness of
.
is not
near
;
is compact, then
is not
in
is not so smooth, let us consider
is smooth at neighborhood
of
and
is positive definite in
.
is simply connected complete manifold with
, then
is
on whole
and
is positive definite on
.