Lemma 1: 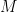 is a Riemannian manifold.
is a Riemannian manifold.  ,
,  neighborhood
neighborhood 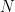 of
of  and
and  such that
such that  is a diffeomorphism and any two points in
is a diffeomorphism and any two points in 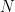 can ve connected by a unique geodesic with length smaller than
can ve connected by a unique geodesic with length smaller than  .
.
Lemma 2: 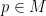 ,
,  is small enough such that
is small enough such that  is a differeomorphism, then for any
is a differeomorphism, then for any  ,
,  such that
such that

Proof:  is a continuous function on
is a continuous function on  . Since
. Since  is compact, then
is compact, then  such that
such that

Suppose  is a minimizing sequence of
is a minimizing sequence of  . For any
. For any  , there exists
, there exists  , then
, then

Letting  ,
,  . By the triangle inequality,
. By the triangle inequality,


Thm(Hopf-Rinow) The following statements are equivalent for Riemannian manifold 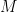 :
:
(1) 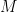 is a complete metric space, where the metric is induced by
is a complete metric space, where the metric is induced by

(2)The closed and bounded sets of 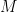 are compact.
are compact.
(3) such that
such that  is defined on all of
is defined on all of  .
.
(4)  ,
,  is defined on
is defined on 
Furthermore, each of the statements  implies
implies
(5) Any two points  can be connected by a geodesic of shortest length. Proof: Let us prove
can be connected by a geodesic of shortest length. Proof: Let us prove  firstly.
firstly.
By lemma 2, there exists 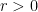 and
and 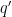 on
on  such that
such that

Suppose  for some
for some  ,
,  , then
, then  is defined on
is defined on 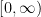 by assumption. Consider
by assumption. Consider ![{\{t|t\in [r,d(p,q)]\}}](https://s0.wp.com/latex.php?latex=%7B%5C%7Bt%7Ct%5Cin+%5Br%2Cd%28p%2Cq%29%5D%5C%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) satisfies
satisfies

denote such points as 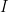 .
. 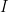 is nonempty as
is nonempty as  and it is closed by the sake of continuity.
and it is closed by the sake of continuity.
Suppose  . If
. If  , we are done. Otherwise consider
, we are done. Otherwise consider  , by lemma 2,
, by lemma 2,  small enough,
small enough,  such that
such that

then

We are going to prove  . From the triangle inequality
. From the triangle inequality


then we must have  . Then the union of
. Then the union of ![{\gamma([0,t_0])}](https://s0.wp.com/latex.php?latex=%7B%5Cgamma%28%5B0%2Ct_0%5D%29%7D&bg=ffffff&fg=000000&s=0&c=20201002) and the geodesic from
and the geodesic from 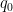 to
to 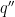 constitutes a shortest curve from
constitutes a shortest curve from  to
to 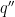 , therefore it must be a geodesic. By lemma 1, such geodesic is unique with given initial values. So it must concider with
, therefore it must be a geodesic. By lemma 1, such geodesic is unique with given initial values. So it must concider with  in the
in the  , which means
, which means  . Then
. Then

This contradicts the fact 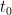 is maximal. So
is maximal. So 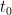 must be
must be  , and the curve
, and the curve ![{\gamma([0,t_0])}](https://s0.wp.com/latex.php?latex=%7B%5Cgamma%28%5B0%2Ct_0%5D%29%7D&bg=ffffff&fg=000000&s=0&c=20201002) is just the minimal geodesic connects
is just the minimal geodesic connects  and
and  .
.
 Evidently
Evidently
 Suppose
Suppose 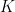 is a bounded set in
is a bounded set in 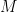 . From
. From  we know,
we know, 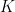 can be contained in
can be contained in  where
where  for some
for some  large enough. Since
large enough. Since  is compact and
is compact and  is a continuous mapping, then
is a continuous mapping, then  is compact, therefore its closed subset
is compact, therefore its closed subset 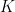 is compact.
is compact.
 Any cauchy sequence in
Any cauchy sequence in 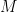 is bounded, its closure is compact by
is bounded, its closure is compact by 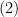 . Then it must have a converge subsequence and being cauchy, it has to converge itself.
. Then it must have a converge subsequence and being cauchy, it has to converge itself.
 For any
For any 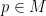 , we need to prove
, we need to prove  is defined on
is defined on 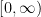 for any
for any  . Consider
. Consider  and
and  is defined on each
is defined on each 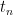 , denote
, denote  .
.
Since  ,
,  is a cauchy sequence,
is a cauchy sequence,  such that
such that  . Since there exists a neighborhood of
. Since there exists a neighborhood of  , say
, say  , such that
, such that  , any geodesic starting from
, any geodesic starting from  can be extended at least up to length
can be extended at least up to length 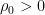 .
.
For sufficiently large  ,
,  and
and  .
. ![{\exp_ptv|_{[t_n,t_{n+1}]}}](https://s0.wp.com/latex.php?latex=%7B%5Cexp_ptv%7C_%7B%5Bt_n%2Ct_%7Bn%2B1%7D%5D%7D%7D&bg=ffffff&fg=000000&s=0&c=20201002) is a curve starting from
is a curve starting from  , then it can be extended at least up to length
, then it can be extended at least up to length 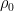 . By the uniqueness of geodesic,
. By the uniqueness of geodesic,  can be extened beyond
can be extened beyond  , namely
, namely  is well defined. So
is well defined. So  is defined on whole
is defined on whole 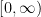 .
.

Remark: Should thank Bin Guo’s picture
,
, prescribe the ball with metric
. We want to use the formula of mean curvature under the conformal transmformation. Namely, suppose the
has mean curvature
, then under metric
, the mean curvature of
will be
is the normal outer unit vector under
. Using the above principle, let
,
be the Euclidean flat metric, then
.